0x0G is Google’s annual “Hacker Summer Camp” event. Normally this would be in Las Vegas during the week of DEF CON and Black Hat, but well, pandemic rules apply. I’m one of the organizers for the CTF we run during the event, and I thought I’d write up solutions to some of my challenges here.

gRoulette is a simplified Roulette game online. Win enough and you’ll get the flag. The source code is provided, and the entire thing is run over a WebSocket connection to the server.

gRoulette

Examining the websocket flow, we series of messages:

1
2
3

{"message_type":"register","balance":100,"round_id":1991705954}
{"message_type":"round_result","round_result":{"roundid":1991705954,"space":"31","next_roundid":520308631}}
{"message_type":"round_result","round_result":{"roundid":520308631,"space":"8","next_roundid":439000315}}

Taking a look at the source code, we see that the rounds are handled by a function in roulette.go:

1
2
3
4
5
6
7
8
9
10
11
12
13

func (g *RouletteGame) PlayRound() {
  ...

	// Finish the round
	finishedRound := g.CurrentRound
	space := g.NextSpace()
	g.CurrentRound = g.prng.Next()
	res := &RoundResult{
		RoundID:     finishedRound,
		NextRoundID: g.CurrentRound,
		Space:       space,
	}
	...

This tells us the space where the “ball” lands is computed using a NextSpace function:

1
2
3
4
5
6
7

func (g *RouletteGame) NextSpace() SpaceID {
	num := g.prng.BoundedNext(37)
	if num == 37 {
		return "00" // Special case double 0.
	}
	return SpaceID(fmt.Sprintf("%d", num))
}

Of interest is that both the CurrentRound and Space values are derived from the same PRNG instance. Depending on the security of the RNG, it may be possible to predict the next space(s) based on the current state of the RNG. The source of the PRNG is provided as well:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

package main

import (
	"crypto/rand"
	"encoding/binary"
)

const (
	PrngModulus    uint32 = 0x7FFFFFFF
	PrngMultiplier uint32 = 48271
)

type PRNG uint32

func NewPRNG(seed uint32) *PRNG {
	if seed == 0 {
		if err := binary.Read(rand.Reader, binary.BigEndian, &seed); err != nil {
			panic(err)
		}
	}
	p := PRNG(seed)
	return &p
}

/*
 Algorithm certified by Nanopolis Gaming Commission
*/
func (p *PRNG) Next() uint32 {
	tmp := uint64(*p) * uint64(PrngMultiplier)
	tmp %= uint64(PrngModulus)
	*p = PRNG(tmp)
	return uint32(tmp)
}

func makeBitmask(v uint32) uint32 {
	rv := uint32(0)
	for v != 0 {
		rv = rv << 1
		rv |= 1
		v = v >> 1
	}
	return rv
}

func (p *PRNG) BoundedNext(max uint32) uint32 {
	mask := makeBitmask(max)
	for {
		tmp := p.Next() & mask
		if tmp <= max {
			return tmp
		}
	}
}

The Next method is responsible for advancing the PRNG. It multiplies by a constant, then takes a modulus. Searching for the constants reveals that this is an implementation of a well-known Linear Congruential Generator. This implementation is similar to the MINSTD RNG, and exposes the entire state in a call to Next. Notably the RoundID is entirely an output of the PRNG, so every subsequent value can be known. Consequently, we can call the PRNG with our own inputs to find out what the next spins will be.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

package main

import (
        "fmt"
        "os"
        "strconv"
)

func main() {
        seed64, err := strconv.ParseInt(os.Args[1], 10, 32)
        if err != nil {
                panic(err)
        }
        round := uint32(seed64)
        p := NewPRNG(round)
        for i := 0; i < 8; i++ {
                roll := p.BoundedNext(37)
                v := fmt.Sprintf("%d", roll)
                if roll == 37 {
                        v = "00"
                }
                fmt.Printf("%d: %s\n", round, v)
                round = p.Next()
        }
}

When we run it, this will print out the next 8 rolls:

1
2
3
4
5
6
7
8
9

% go run . 520308631
520308631: 8
439000315: 0
2059893773: 33
1060020398: 5
1254119902: 32
1689320946: 2
918638365: 28
114073520: 20

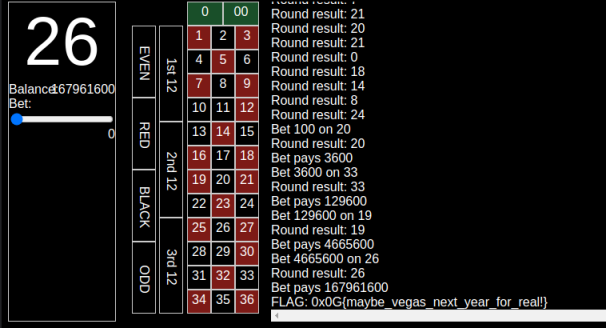
Just max bet each one and you’ll have the requisite money in no time. :) (Feel free to automate it. I just did it manually.)

1

FLAG: 0x0G{maybe_vegas_next_year_for_real!}

gRoulette Solved